What is P vs NP?
To understand the problem, first the definitions of P and NP must be understood. Many computer scientists like to look at a problem in terms of how hard it is to solve. This can depend on two things, the input size and the complexity of the problem. Rather than checking how time compares with the calculation, mathematician John Nash suggested we look at how the computation grows in relation to input size. The computation is measured in ‘machine operations’ or ‘steps’ to solve a problem. We call this "Big O notation.” The progression in steps due to input size can then be graphed:
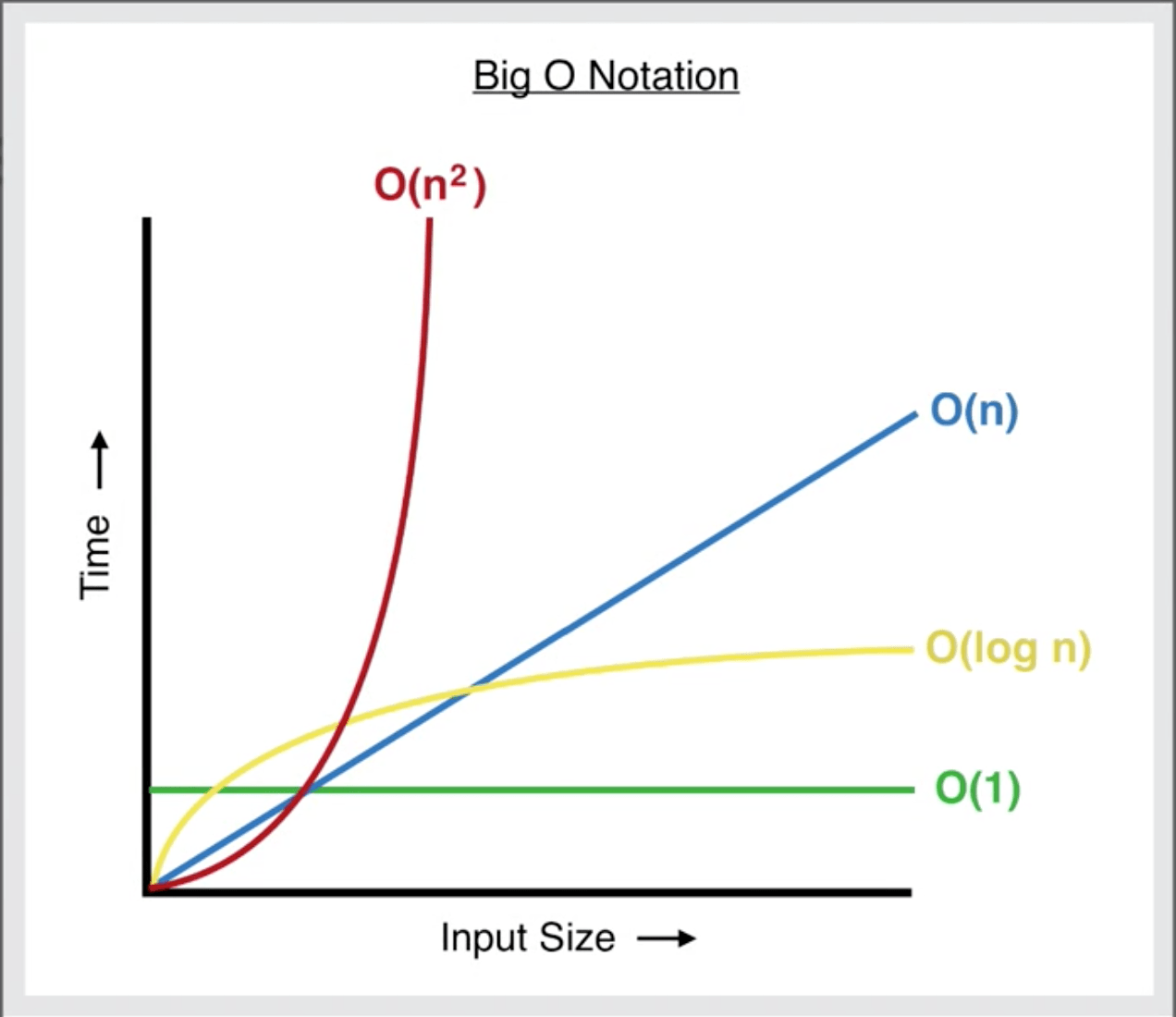
Some problems grow in complexity faster than others. For example addition grows a lot slower than multiplication which each increase with input (digit) size. We know this too because of how long it takes us to do written multiplication and addition. Problem complexity often depends on the number of iterations (loops) it takes to solve a problem. Easier problems will just take a simple increase in iterations to solve and this results in what is known as ‘linear time growth’ as shown. However more complicated problems may involve ‘nested’ iterations (loops inside loops) and when the input size increases, the number of steps to solve increases by a greater rate as shown. This can be graphed as n2. It was therefore suggested these types of problems are classified as ‘polynomial time’ or ‘P.’
Most problems a computer is asked to solve uses polynomial time. However a different type of problem can cause a computer more issues – exponential problems. If you asked a computer to brute force solve a password, every time a digit is added it would exponentially grow the number of combinations it must try. This growth is referred to as ‘exponential time’ and is graphed as a much steeper curve kn. These problems would require so much time for a computer to solve, they are categorised as being impractical. However some computer scientists have been able to find smart solutions and shortcuts to exponential problems which have reduced them from the exponential category to the polynomial category:
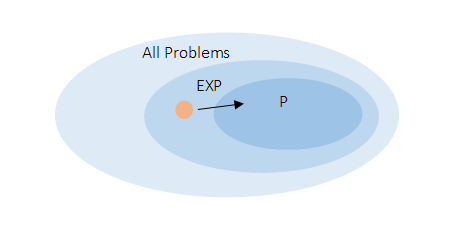
However some exponential problems seem too complicated to ever be simplified. Later though, computer scientists noticed patterns linking many of the exponential problems to polynomial problems. This was problems which seemed very difficult to solve, suddenly appeared to be very simple once the solution was obvious. This is evident in many riddles. These types of problems were categorised with the name ‘NP.’
NP problems are easy to verify but difficult to solve. For example, knowing the roots to a polynomial is easy to verify and check they work, however finding them is much more difficult. NP stands for “non-deterministic polynomial time” meaning people theorised these problems could be solved in polynomial time using a non-deterministic machine. This is a theoretical machine which transitions from one state to multiple states simultaneously unlike deterministic machines:
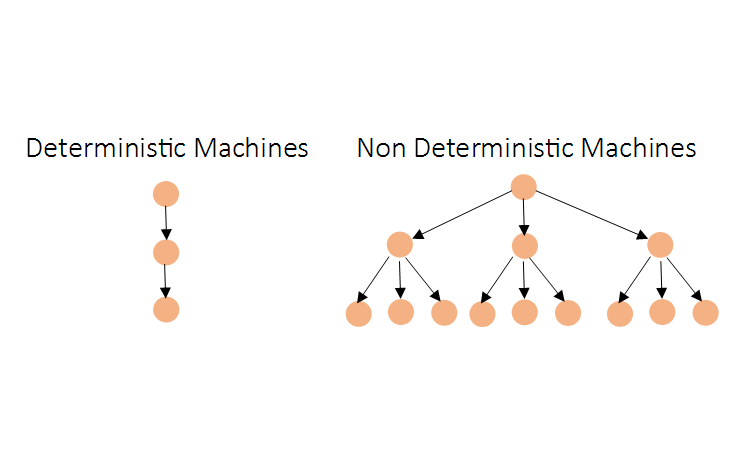
NP problems make up a vast quantity of problems we face today, even outside of the computer science and maths realm. However since the non-deterministic machine does not exist it is thought that to solve an NP problem it will always take exponential time using regular deterministic machines, therefore P ≠ NP.
However one last thing many computer scientists have recognised is many of the NP problems have very similar structures and qualities. This means many of the problems can be ‘reduced’ to each other. This set of connected problems is known as ‘NP complete.’ If any one of these NP complete problems could be solved using polynomial time, then all these problems could be solved using polynomial time, therefore P = NP. The P vs NP problem is the most popular question in the computer science industry and there is a $1,000,000 prize for the first correct solution.