Information Theory

Entropy

Suppose you had a coin in your left hand and a single letter in your right hand and I ask you this simple question, ‘In which hand are you holding more information?’ You may instantly say your right hand, but why? What exactly is information and how is it comparable. To answer this I present to you Claude Shannon, an American mathematician, often dubbed ‘the father of information theory.’ Shannon devised the term ‘information entropy’ which is a method of measuring the information in a given system based on the ‘uncertainty’ of its state. A good way to measure entropy is to answer the following question:

“What is the least amount of yes/no questions I would have to ask before I know the state of my system?”

Lets use our example of the coin and the letter. With the coin you could simply ask if it is a heads. If the answer is a yes, then you know its state. If the answer is no, you know the coin is a tails and therefore still know its state. Hence, a coin has an entropy of 1. On the other hand a letter has twenty-six possible states. The most efficient method to find the state of the letter is by using a binary search strategy. Is the desired letter to the left of the midpoint in the alphabet? If so, discard the letters to the right of the midpoint and if not discard the letters to the left. Repeat this process until you have found the letter. Using this method, a letter, on average has an entropy of 4.7. As a result we can conclude the letter stores more information that the coin.

Why is Entropy Important?

Being able to quantise information is incredibly important, especially during the transmission, efficiency and storage of information. Earlier we said the coin had an entropy of 1. However what does this mean in terms of computer science? It means that a coin can be represented by 1 bit of data. In terms of the English language, how much information can we transmit? Obviously we have our 4.7 bit per letter alphabet, however this is based on one grand assumption; the alphabet is random. In the real world, this is definitely not the case. Consider the sentence below:

“hxllx, whxt xs yxxr nxmx?”

The consonants and question mark provide just enough information to compensate for the falsified information and the question is near enough interpretable. The English language is based on many patterns that make information sharing incredibly diverse. For example messages like ‘c u l8r’ and emojis will usually suffice for simple messages. In information entropy, these are called ‘redundancies.’ As a result of redundancies and patterns, information can compressed effectively and this has an enormous effect on many technologies we use today.

Huffman Coding

In 1952 David Huffman was able to design an algorithm which would use these frequency patterns in the English language to compress text. A very key element of text compression is that it must be ‘lossless’ compression, otherwise the information will not be the same and could be misinterpreted. This is the general process:

All the letters, characters and spaces in a text document are counted and ordered from highest to lowest. As you might imagine, a space and the letter ‘e’ appears high in the list whilst a ‘q’ and ‘x’ appear much lower.
The bottom two characters are the combined in a tree like structure:

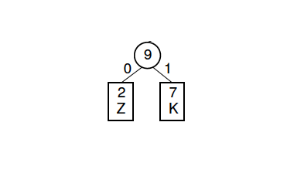
Section of a Huffman Tree

This process is repeated with the bottom two elements every time until the last two elements are combined and a grand tree structure has formed. This is also known as a ‘Huffman Tree.’
Each left branch is labelled as 0 and each right branch is labelled as 1. It should look like the example below:

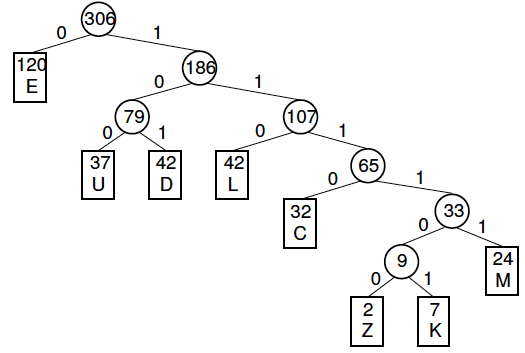
Huffman Tree Diagram

Each character in the text document can then be encoded using the path required down the tree to reach it. In this example, the letter ‘L’ would be encoded as ‘110.’
The tree itself must also be transmitted to act as a key for the data extraction.

Normal data transmission would usually use 7 or 8 bits per letter. By compressing the data and utilising the redundancies, we are able to send much more data with much less medium. This is useful in a variety of different processes within computer systems. The same idea is applicable to the compression of sound and video, meaning high quality media with a lot of information and high entropy can be transmitted with the least amount of bandwidth possible.